Calculating section factors

The section factor of an unprotected hot rolled open section, hot finished/formed hollow section or fabricated girder is defined as the surface area of the member per unit length (A_m) divided by the volume per unit length (V). It is measured in units of m^-1. For members which are not exposed on all sides, for example if a beam supports a concrete slab which protects the top surface of the upper flange, the value of A_m is taken as the heated surface exposed to fire. The section factor might equally be defined as the heated perimeter, H_p, divided by the cross-sectional area, A. This latter definition may be found in older guidance. Section factors vary from 17 m^-1 for very large sections to over 300 m^-1 for small, slender sections.

Calculation of section factors for exposed sections

Extract from The Blue Book showing dimensions used in section factor calculations

Format for presentation of section factors in The Blue Book

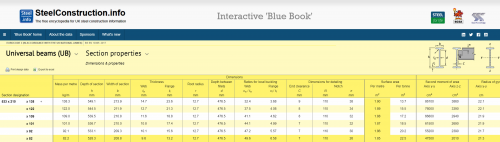
Take the example of a hot rolled open section, a 533 x 210 UB 82 from The Blue Book. If this is exposed in fire on all four sides, the heated perimeter is given by:

A_m = 2h + 4b + 2πr - 8r - 2t_w

where h, b, r and t_w are defined as shown to the right.

(2 x 528.3) + (4 x 208.8) + (π x 12.7 x 2) – (8 x 12.7) – (2 x 9.6) = 1851 mm or 1.851 m

The heated perimeter of an unprotected section can be extracted directly from the table, as it is the same value as the surface area per metre, given as 1.85 m

The cross-sectional area from The Blue Book is 105 cm² or 105E-4 m²

The section factor is therefore 1.851 / 105E-4 =176.3 m^-1

This is usually rounded a whole number. The section factor is therefore 176 m^-1.

This is correct if the beam is unprotected or if the form of fire protection follows the profile, for example, a spray or an intumescent coating.

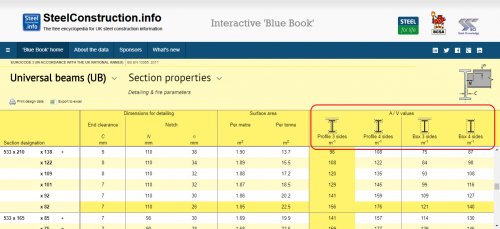
If the fire protection forms a box around the section, such as a board, then the heated perimeter becomes:

A_m = (2h + 2b)

(2 x 528.3) + (2 x 208.8) = 1.474 m and the section factor is 1.474 / 105E-4 = 140.4, which is given as 140 m^-1 in the Blue Book.

If the beam is carrying a concrete floor slab which shields the top flange, the heated perimeter for unprotected beams or beams with profile protection is:

A_m = 2h + 3b + 2πr - 8r - 2t_w

(2 x 528.3) + (3 x 208.8) + (π x 12.7 x 2) – (8 x 12.7) – (2 x 9.6) = 1.642 m

The section factor is therefore 1.642 / 105E-4 =156.4 m^-1, which is given as 156 m^-1 in the Blue Book.

If the beam is carrying a concrete floor slab which shields the top flange, the heated perimeter for protection forming a box around the section is:

A_m = (2h + b)

(2 x 528.3) + (208.8) = 1.265 m

The section factor is therefore 1.265 / 105E-4 =120.5 m^-1, which is given as 121 m^-1 in the Blue Book.

Section factors for the full range of open sections are calculated in the The Blue Book and are provided in the format shown.

Calculation of section factors for partially exposed sections

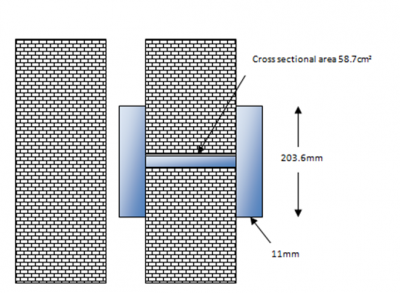
Where sections are partially exposed, the section factor is calculated based on the full cross-sectional area but the exposed perimeter only. One of the most common situations where this occurs is with columns in perimeter walls. For the example shown, which is a 203 x 203 UC 46:

Heated perimeter = 203.6 + (11 x 2) = 225.6 mm

The section factor is = 0.2256 / 58.7E-4 = 38 m^-1.

It should be noted that the calculation method in Table 4.2 of BS EN 1993-1-2 uses a more conservative value for the section factor as calculated by division of the exposed steel perimeter [A_exp] by the exposed steel cross section area [V_exp] rather than the entire volume of the steel section, despite the fact that heat is conducted into the entire volume of the steel section and also into the mass in contact with the embedded steel surface.

Thus, for partially exposed unprotected steel, the Eurocode section factor (A_m / V) = (A_exp / V_exp).

For the purposes of this calculation, the section factor would be (0.2036 + (2 x 0.011)) / (0.2036 x 0.011) = 101 m^-1.

Resources

• Steel construction - Fire Protection supplement, 2013
• SCI P363 Steel Building Design: Design Data, 2013
  A web-based interactive version of the 'Blue Book', is also available.

Further reading

• Fire protection for structural steel in buildings 5th edition (The Yelllow Book). Published by the Association for Specialist Fire Protection.

See also

• Car parks in fire
• Fire protecting structural steelwork

External links

• Association for Specialist Fire Protection

CPD

• Design for fire
• Fire engineering seminars 2013